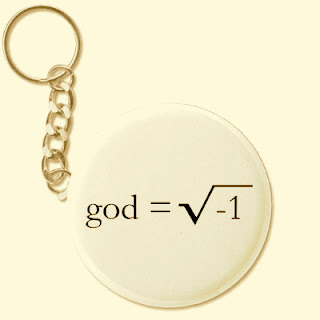Carnaval del número "i"

Antes del Carnaval, un poco de número i para llegar como conviene al baile de disfraces*. La fórmula raiz cuadrada de menos uno es un modo, bello y muy interesante, de intentar escribir algo que no existe pero que no por ello deja de tener un estatuto imaginario. En efecto, no existe ningún número real que elevado al cuadro sea igual a -1. Pero hete aquí que el lenguaje, y no otra cosa, nos permite hacer existir el número i para designar, entre otras, esa falta irremediable. Y lo más interesante es que puedo operar con él y explicar además ciertos fenómenos de lo real operando con él.

Según me informan, fue un tal Bombelli quien en el siglo XVI ideó los números imaginarios, aunque sin llegar a designarlos así. Los llamaba piu di meno, más que menos, curiosa designación. Es del siempre fecundo Descartes que procede el término imaginario para dichos números, a partir de su frase referida al intento de resolver ciertos polinomios: on peut imaginer…
Detengámonos un poco más en este enigmático número i, en esta imposible raíz cuadrada de menos uno que un Leibniz llegó a calificar de "anfibio entre el ser y la nada", en esta feliz creación del lenguaje de la que no existe, a priori, referente real alguno. Exiliado de lo real, su condición de imaginario no lo convierte en irreal ni en un simple argumento para fraudes engañosos. Nadie ha visto, en efecto, un número i paseando por la calle, ni científico alguno ha podido verificar hasta hoy en día su existencia empírica y objetiva. Ni es ni no es, y sin embargo eso no le impide ser de lo más operativo para dar cuenta, por ejemplo, de ciertos fenómenos de la Física. Es una ficción del lenguaje, pero un ficción operativa, con efectos sobre ese mismo real en el que no ha encontrado ni encontrará nunca su causa.

Pues bien, estimados escépticos, un concepto tan operativo para el psicoanálisis como el de falo simbólico no tiene en realidad una condición tan distinta. Ese falo, que Freud empezó a escuchar a diestro y siniestro como el que se encontraba a faltar en el cuerpo de la madre o de las demás mujeres, ese falo que los psicoanalistas de hoy en día siguen escuchando en la intimidad de su consultorio - cuántos testimonios de sujetos, niños y menos niños, masculinos y femeninos, sobre ese falo que supusieron y esperaban encontrar hasta edades bastante avanzadas - ese falo es también una creación del lenguaje de la que no existe, a priori, referente real alguno. Exiliado también de lo real, su condición de imaginario (aunque en un sentido no exactamente igual al matemático) no lo convierte en irreal ni en un simple argumento para fraudes engañosos. Ni es ni no es, anfibio entre el ser y la nada, pero lo escuchamos pulular en fenómenos tan dispares como el fetichismo, el trasvestismo, y también en las fantasías más banales e íntimas de la vida sexual común…

Tal vez con más suerte que los matemáticos y su número i, tenemos la oportunidad de "verlo” también en la calle, especialmente cuando sirve para ataviar al sujeto en las más barrocas florituras destinadas a esconder lo que falta y a sugerir lo que no existe detrás del velo, en el juego de mostrar y esconder tan propio del carnaval de la vida. Y eso hasta tener verdaderas propiedades afrodisíacas.

En fin, si alguien quisiera seguir el baile de lo real, de lo simbólico y de lo imaginario en el Carnaval de los sexos, nada mejor que la referencia de un Alphonse Allais y su ”Un drama muy parisino”, pequeño cuento para amantes de la lógica del falo en el malentendido entre los sexos…

Podéis leerlo aquí:

Un drama muy parisino

Fue un referencia que Jacques Lacan daba a veces para estudiar la función del "semblante", de la máscara y del falo en la sexualidad.

*Respuesta a un científico en un debate sobre el inconsciente y el número i.

De matemáticos, ajedrecistas y psicoanalistas

La invitación al debate de nuestra Presidenta Lucía D’Angelo* me ha llegado cuando recibía a la vez un interesante texto que acaba de publicarse en su traducción catalana. Se trata de A Mathematician’s Apology , “Apología de un Matemático”, escrito en 1940 por Godfrey Harold Hardy, ilustre matemático inglés especialmente dedicado a la matemática pura. Su lectura me parece más que aconsejable después de la referencia que Jacques-Alain Miller dio en su primer curso de este año, Choses de finesse en psychanalyse, el pasado 12 de Noviembre, en relación a la diferencia entre matemática pura y matemática aplicada para centrar nuestro debate actual entorno al psicoanálisis puro y aplicado.
Va una cita del texto de Hardy en su defensa de la matemática pura: “Creo que podría reforzar mi argumento apelando a los sentimientos de los propios jugadores de ajedrez. Seguro que un maestro de ajedrez que juega grandes partidas en torneos importantes, en el fondo, desdeña el arte puramente matemático subyacente en los problemas de ajedrez. El jugador guarda el arte matemático como una reserva que puede utilizar en una emergencia”. La idea de Hardy es que la matemática pura, - la “auténtica”, llega a decir -, puede quedar entonces desdeñada, y hasta olvidada, en las aplicaciones que hacen de ella los físicos o las técnicas que encuentran su utilidad inmediata. Al maestro de ajedrez evocado por Hardy puede ocurrirle lo que a aquellos panaderos evocados por Richard Sennett y citados por nuestra colega Mercedes de Francisco en la última Jornada Ripa en Barcelona: saben apretar los botones para hacer pan, pero no saben ya cuál es el noble arte de hacer pan. El ganador de la partida de ajedrez sabe hacer los movimientos para hacer jaque mate después de haber memorizado muchos finales de partida, como hizo la máquina Deep Blue frente a Kasparov, pero puede llegar a desdeñar el arte matemático que subyace en la lógica de esos movimientos. Y puede ocurrirle entonces algún día lo que le ocurrió a los personajes del cuento de Ray Bradbury evocado por Jacques-Alain Miller en la misma Jornada Ripa, esos personajes que con sus grandes ordenadores habían olvidado cómo tratar un problema que alguien vino a resolver finalmente con un lápiz y un papel.
El problema no es banal y la caricatura que supondría poner en serie con estos personajes un practicante actual del psicoanálisis, - ese que podría olvidar su noble arte con sus aplicaciones terapéuticas - no debe escondernos la verdadera naturaleza del problema, que es el de la naturaleza misma del psicoanálisis.
Pero sigamos todavía un poco más la argumentación por el lado de la matemática, para ver qué puede enseñarnos. En la excelente Introducción a la edición catalana de la obra de Hardy, el matemático Josep Pla escribe algo que puede parecer sorprendente: “No hay que confundir la matemática aplicada con la aplicación de la matemática (...) La matemática aplicada es matemática, forma parte de lo que se incluye semánticamente en la palabra matemática. Las aplicaciones de la matemática son los usos, más o menos restringidos, que de la matemática hacen los físicos – aquí es donde hay que ir con pies de plomo –, los ingenieros, los arquitectos, los informáticos, los biólogos, los sociólogos y muchos otros científicos. Un matemático aplicado, insisto, hace matemática”. Es algo tan esclarecedor como aparentemente tautológico. Entonces, un físico, por ejemplo, no hace de hecho matemática – ni pura ni aplicada – sino que aplica la matemática de manera restringida a fenómenos que en realidad no son fenómenos matemáticos. Pero entonces, sólo el matemático hace realmente matemática aplicada cuando aplica la matemática con toda su potencialidad... ¡a los fenómenos propiamente matemáticos!
La conclusión de Hardy siguiendo esta línea de argumentación es de lo más jugosa: “Todo esto puede parecer evidente, sin embargo es bastante confuso ya que las materias más ‘útiles’ muchas veces son las que parecen más inútiles cuando las aprendemos (...) Por mi parte, nunca me he encontrado en ninguna situación en la que mis conocimientos científicos, al margen de los que tengo en matemática pura, me hayan servido de algo” (las itálicas son nuestras). Finalmente, la mayor utilidad no es la que se deriva de las aplicaciones de la matemática en sus usos restringidos sino la que el matemático Hardy ha encontrado en la matemática pura, aquella que permite ser aplicada a los propios fenómenos matemáticos.

Debo confesar que la argumentación me parece impecable y que tal vez puede enseñarnos algo para nuestro debate.
¿No convendría distinguir también, por nuestra parte, el psicoanálisis aplicado de las aplicaciones del psicoanálisis, de los usos, más o menos restringidos, que hacemos del psicoanálisis en sus diversas potencialidades? Por ejemplo, – y llego así a uno de los puntos claves de nuestro debate –, la aplicación que hacemos del psicoanálisis en los Cpct es un uso restringido, dosificado, del psicoanálisis a “consultas” y “tratamientos” específicos, es una aplicación con la que producimos, siempre por añadidura, efectos terapéuticos. Conviene no olvidar, en efecto, que lo terapéutico es aquí también un efecto colateral – un “daño colateral”, me atrevería a decir – y no tanto el campo específico de la aplicación. Y lo más útil desde el punto de vista de la demanda social no es, no debería ser en realidad, lo más interesante y útil desde la perspectiva del propio psicoanálisis. Lo más útil para el psicoanálisis es lo que parece más inútil para la demanda social en las “consultas y tratamientos”, lo más útil para nosotros es lo que de todo eso podemos aplicar al propio psicoanálisis.
¿Sería exagerado decir por nuestra parte que el psicoanalista sólo hace psicoanálisis aplicado cuando aplica el análisis a los fenómenos propiamente analíticos? Me parece una perspectiva interesante. Y tal vez es lo mejor que deberíamos esperar de un analista en la Escuela.
Veo así un beneficio en esta forma “matemática” de argumentación. Y es que nos hace más presente la pregunta, que nunca debería parecernos evidente ni ya respondida en una Escuela: ¿Qué es un psicoanalista? O bien, según al expresión de Lacan: lo que el psicoanálisis nos enseña, ¿cómo enseñarlo?

En eso estamos. Y es por este sesgo que lo que llamamos psicoanálisis puro, entendido como una experiencia y no como una terapéutica, tiene hoy su mayor razón de ser. Pero esto puede ser ya motivo para otra contribución al debate.

*Este texto ha sido una contribuión al debate impulsado por la Presidenta de la Escuela Lacaniana de Psicoanálisis (ELP) en su Lista ELP-Debates.